“Uncertainty is an uncomfortable position, but certainty is an absurd one.”

-Voltaire^[1]

Probability is a way of thinking about chance that people use often in their daily lives. Probabilities are always between 0% and 100%, with something that is impossible having a probability of 0%, and something that is certain having a probability of 100%. Probabilities between these two extremes represent uncertainty; when you say something has a twenty-five percent probability, you expect it to happen about a quarter of the time.

Just like we can choose Kelvin, Celsius, or Fahrenheit scales to measure temperature, we can choose other scales for measuring chance besides probability, and these can be easier to think about in some situations. One such alternative measure of chance called log-odds has some very useful properties.

Instead of going from 0% to 100% like probability, log-odds covers all the real numbers, from negative infinity to positive infinity. Something that is absolutely certain (100% probable) has log-odds of infinity, while something that is absolutely impossible (0% probable) has log-odds of negative infinity. Log-odds greater than zero correspond to things that are more than 50% probable, while log-odds less than zero are less than 50% probable. In the middle, log-odds of zero means the same thing as a fifty-fifty chance. The common units of log-odds are called decibans^[2]:

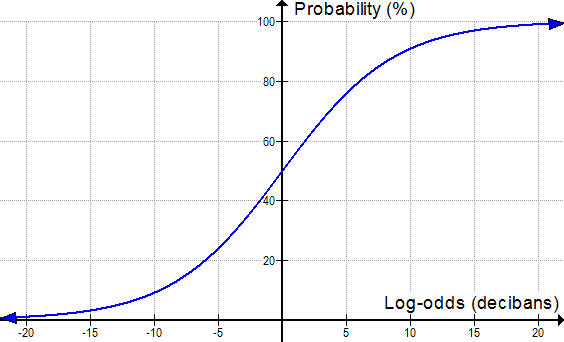
Some numbers, such as “110%” or “-20%”, aren’t valid probabilities at all, since there can never be something that tends to happen more often than always, or less often then never. One of the nice things about thinking in terms of log-odds is that any number between negative infinity and positive infinity is always valid. We don’t have to remember that some numbers aren’t valid because we can’t even write down a number corresponding to greater than certainty.

Another nice thing about thinking in log-odds is that it makes very large and very small probabilities easier to visualize. Human beings are good at understanding moderately-sized numbers, but tend to lose the intuitive meaning of numbers that are very large or very small. (Can you really visualize the difference between one-in-a-million and one-in-a-billion?) Log-odds keeps the numbers more manageable:

Even really small probabilities can be expressed conveniently in log-odds. The log-odds of a monkey at a typewriter randomly typing out the complete works of Shakespeare on its first try is about -120 million decibans. If you wanted to write this out as a decimal probability instead of using log-odds, you’d actually need more paper than Shakespeare needed to write down his plays in the first place.

But perhaps the most elegant property of log-odds is the way it can be used to visualize the connection between evidence and beliefs^[6]. When you observe a new piece of evidence that supports or opposes some hypothesis about the world, that new observation should increase or decrease your degree of belief in that hypothesis (this is called a “Bayesian update”). If you use probability you have to plug the probabilities into Bayes formula and crunch the numbers to get the new probability that the hypothesis is true.

With log-odds, this is easier to visualize. Observations that support a hypothesis will have a positive number of decibans, and observations that oppose a hypothesis will have a negative number of decibans. This corresponds to moving toward the right and moving toward the left in the graph below. If your initial belief (your prior) is -2 decibans (~39% probability) and then you do an experiment that gives you 5 decibans of support for your hypothesis you end up at +3 decibans (~67% probability). If you repeat the experiment and get the same result (and if the two experiments are independent), it will shift you another 5 decibans to the right, to +8 (~86% probability):

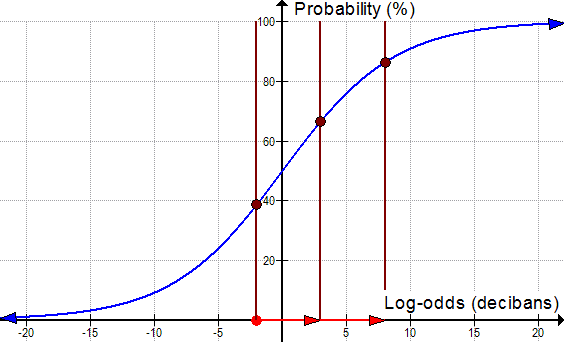
Visualizing the effect of obtaining new evidence by thinking about the graph above provides a good intuitive picture of how Bayesian reasoning works. All you have to do is add together the number of decibans that all your observations constitute and you know how much your degree of belief should be shifted by. Supporting evidence moves you to the right, opposing evidence moves you to the left. If you observe more and more supporting evidence, these push you farther and farther toward the right, and your degree of belief gets closer and closer to 100%.

It’s worth noticing; however, that we never actually get to 100% certainty though, no matter how much strong evidence we observe. Thinking in terms of log-odds reminds us that all ideas in science are tentative to some degree, and could have to be revised in light of strong enough opposing evidence. As we observe more and more supporting evidence for an idea, our degree of belief in the truth of that idea gets closer and closer to 100%, but it never actually gets there. This is an yet another example of how probability theory can give us new ways to answer philosophical questions about foundational issues in science.

Thinking in decibans gives us a powerful way to visualize what should happen to our beliefs as we make observations that carry information relevant to those beliefs. It makes our degree of belief linear with the observations we make, so it lets us easily visualize the effect of observing new evidence as simply shifting our beliefs toward certainty or toward impossibility. Thinking in decibans also reminds us that we can never actually reach certainty in any belief, since that would require us to observe infinitely strong evidence. We only approach certainty more and more closely as we make observations that support our hypothesis.

Share