The idea of measurement, of using numbers to describe the properties of things, is a central part of science. Measurement is what lets us characterize things precisely and repeatably enough that we can see the rules working behind the scenes, the laws of the universe that determine how everything happens.
Measurement allows us to take our everyday perceptions, like “the giraffe is tall” or “the coffee is hot” and free them from our subjective judgments. To do this we make them precise by quantifying them, like “the giraffe’s height is 5.3 meters” or “the coffee’s temperature is 80ºC”. If you can measure these then you can make objective statements about how tall or hot things are.
Clearly when we use words like “hot”, “temperature”, and “degrees Celsius” we are talking about some concepts that are closely related. In science education the concept of a physical quantity is so basic that it is rarely defined explicitly, and students’ understanding of the concept is usually taken for granted. The even more basic concept of a physical quality is discussed more rarely still, but it is an interesting exercise to unpack and explore these concepts to gain a deeper understanding of what are, after all, some of the foundational ideas in science.
A quality is a property or an attribute of something, such as “hot”, “tall”, “heavy” or “likely”. It is useful to think of pairs of opposite qualities, like cold and hot, as being the two directions along a line. Every possible degree of coldness or hotness then lies somewhere along this line, called the cold-hot quality space. Without yet talking about the quantity temperature, it is possible for us to know when one thing is hotter than another, and even to identify some special points along this quality space, such as the melting point of ice:

When we say something like “the coffee is hot” there are no numbers involved, we simply recognize that some things are hotter and some things are colder. This idea of a physical quality is more fundamental than the idea of a physical quantity. In fact, the cold-hot quality was discussed by Aristotle nearly 2000 years before the quantity “temperature” was first introduced by Galileo in the 1590s[1].
To define a physical quantity, what we do is to come up with a way to attach numbers to each point in a quality space. In the case of temperature there are several different quantities commonly used, such as absolute temperature, Celsius temperature and Fahrenheit temperature. Each of these represents a different way to assign a unique number to each point in the quality space. You can think of a physical quantity as being like a ruler placed next to the quality space:
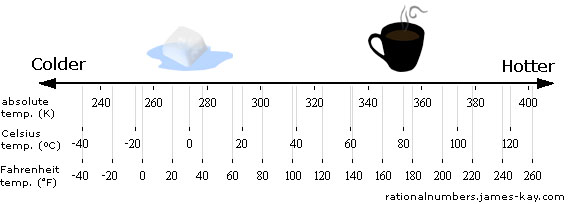
This is the fundamental relationship between a physical quality and a physical quantity. Behind any physical quantity there is an underlying quality space, and a quantity is simply a coordinate system that we have chosen to impose over that quality space. So, weight is a coordinate system over the light-heavy quality space, distance is a coordinate system over the close-far quality space, and probability is a coordinate system over the unlikely-likely quality space.[2]
For any measurable quality[3] there is always more than one quantity that can be used as a coordinate system. For example, since most quantities are represented by a combination of a number and a unit of measurement, one simple way to get a different coordinate system is simply to use a different unit. When we say “the giraffe is 5.3 meters tall”, we mean that 5.3 meters will fit into the giraffe’s height, or equivalently that the giraffe’s height is 5.3 times bigger than a meter.
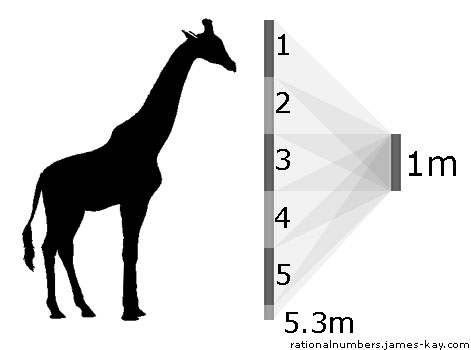
This gives us one possible coordinate system over the close/far quality space, which we call distance in meters. If we choose to use feet as our unit instead of meters, we get a different coordinate system:
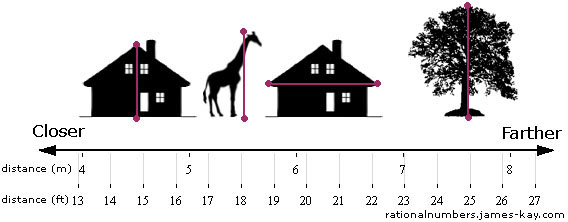
We can also change the way we measure distance in more fundamental ways than just changing the unit. For example, instead of thinking about how many times a meter fits into the height of the giraffe, we could think about how many times the giraffe’s height would fit into a meter[4], which would give us the inverse height. Or we could use the distance squared, a quantity called the quadrance, which is sometimes used when doing trigonometry because it can simplify the math involved.[5]

The quantities we use to measure things can sometimes affect how easy it is to reason about them. This is shown dramatically in an effect called the MPG Illusion. In the US and the UK, fuel efficiency is usually measured in miles per gallon, whereas elsewhere it’s more commonly measured in liters per 100 kilometers. Notice that these are not just using different units but are different ways of measuring the same thing, much like height and inverse height. One tells us how much fuel it takes to drive a given distance, while the other tells us the distance you can drive with a given amount of fuel.
Richard Larrick and Jack Soll conducted an experiment where subjects were asked to rank how much fuel they thought would be saved in different scenarios where a town replaced their current fleet of vehicles with more fuel efficient ones. When the fuel efficiencies were given in miles per gallon, only 25% of subjects were able to correctly choose the scenario that saved the most fuel. When the same problem was presented using gallons per 100 miles, 64% of people chose the best scenario[6].
The concepts of physical qualities and physical quantities are closely related, and are foundational concepts in science. A judicious choice of quantity can not only make the mathematical analysis easier to do, but can also make a problem more natural to think about. Using the most appropriate quantities can be helpful when doing science, and it can literally be the difference between understanding and misunderstanding when we communicate science to the public.
Note: If the reader still doubts that the idea of a physical quality is more fundamental than a physical quantity, consider that physical laws can actually be written as intrinsic theories, meaning they can be written as relationships between physical qualities directly, without reference to any specific physical quantity. For those interested in the details of how intrinsic theories are formulated, Albert Tarantola’s book Elements for Physics – Quantities, Qualities, and Intrinsic Theories is an excellent reference. It is, however, not a book for the nontechnical reader as it requires some rather advanced mathematics such as tensors, group theory, and topology.
