Imagine that I claim to have invented a new test for diagnosing some disease. Unlike many other tests, my test never gives false positives. In statistics we would say that the test is 100% specific; if you don’t have the disease, my test always correctly says you do not have the disease. This may seem like quite a remarkable achievement. Assuming my claims are true, would you rely on this test to diagnose you?
As a matter of fact, you don’t have to merely imagine that I have invented this test, because I actually have invented such a test. My test also has a few other remarkable properties. For example, diagnosis using my test can be performed over the internet. And now, here is your personal diagnosis: congratulations, you do not have the disease!
My test works by simply informing everyone tested that they do not have the disease. My claim that it never gives false positives is true because it never gives positive diagnoses at all. So, clearly, being 100% specific (never giving false positives) is not what makes a diagnostic test useful. Maybe you object that what we really want a test to do is to correctly identify the sick people, not the healthy people. You might say that my test was not useful because the false positive rate is not as important as the false negative rate. My test diagnoses sick people as healthy; perhaps what we want is not a test that is 100% specific, but a test that is 100% sensitive, meaning that it would never identify sick people as being healthy.
Fortunately, I have also invented such a test. Like my other test, it can also be used to diagnose people over the internet, but unlike my first test my second test never identifies a sick person as being healthy. Now using this test, here is your personal diagnosis: Unfortunately, you have the disease!
This bad news likely doesn’t concern you much because, as you have probably guessed, my second test is just as useless as my first test. Unlike the first test, this test never mistakenly identifies a sick person as a well person; however, it also never identifies a well person as a well person.
The fundamental problem with both tests is that you always get the same diagnosis regardless of if you have the disease or not, and so the test results give you no information about the actual state of your health. A highly specific test is one which will usually diagnose you as well if you are well. A highly selective test is one which will usually diagnose you as sick if you are sick. For an observation (like a diagnostic test) to strongly support a hypothesis like ‘you (do/don’t) have the disease’ it needs to be both highly specific and highly selective.
So, finally, imagine there is a disease affecting 1 in 1,000 people. There is a test for this disease that is 90% specific and 90% sensitive. In other words, the test correctly diagnoses 90% of people who have the disease, and correctly diagnoses 90% of people who do not have the disease. Lets say that you have been tested and the test result indicates that you do have the disease. What is now the probability that you have the disease?
Before reading below you may want to try answering the question yourself. Don’t worry about getting it wrong; most doctors get it wrong too.[1]
The probability that you have the disease is…a little less than 1%.
This may be difficult to reconcile with your intuitions at first. How can the probability of being sick be less than 1% if we just observed strong evidence that you do have the disease[2]. What exactly is going on here?
To explain this counter-intuitive result, imagine 10,000 people take the test. Each person is shown as a square in the diagram below. Since 1 in 1,000 people have the disease, there are 10 people out of the total 10,000 who have the disease, and the rest (9,990 people) don’t have the disease. When these 10 people with the disease get tested, the test will tell 9 of them (90% of 10) that they have the disease, and will wrongly tell 1 person that they do not. When the 9,990 well people get tested, the test will tell 8,991 of them (90% of 9,990) that they do not have the disease, and will wrongly tell 999 of them (the other 10% of 9,990) that they do have the disease.
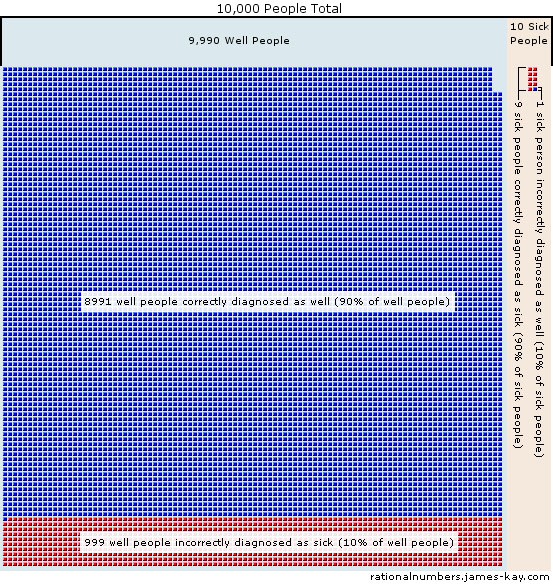
When the problem is put this way, in terms of numbers of people instead of probabilities, people seem to find it much easier to see what’s going on[3]. If you got a positive diagnosis, you know you’re one of the red squares, but most of the red squares are still people who don’t have the disease. Out of a total of 1,008 people who got bad news (represented by red squares), 999 of them do not have the disease, and only 9 people do. There are more healthy people that the test was wrong about than there were sick people that the test was right about. The test does, in fact, constitute fairly strong evidence that a person has the disease: strong enough to raise the probability from 1 in 1,000 to 1 in 112. This final thought experiment illustrates the importance of the third piece of information you need to reason using probability, the prior probability.
Experimental psychologists have discovered that people have a tendency to neglect the prior probabilities and look only at the most recent observation in many situations[4]. This is one reason why it is useful to think about new information as shifting your degree of belief up or down, rather than as new information determining whether something is probable all on its own. The logical fallacy committed when prior probabilities are ignored is called base rate neglect.
If you guessed at the answer to the example above and your guess was 90%, you may be wrong, but you’re in good company. In an experiment involving students and staff at Harvard Medical School, nearly half of the participants also substituted the probability of getting a positive test result if you’re sick, (90% in the example above) for the probability that you are sick if you get a positive test result (less than 1% in the example above)[5]. This is essentially a known bug in our brain’s intuitive reasoning software: we easily confuse the probability of the observation given the hypothesis for the probability of the hypothesis given the observation.
To judge the probability that a hypothesis about the world is correct, you need three independent pieces of information. First you need to know your the prior probability. This is your old probability that the hypothesis was correct, before you made the new observation. Then, to know how strongly the observation supports the hypothesis we require two more numbers. This is because we just don’t care just about what the hypothesis predicts about the world, but we care about the difference between what the hypothesis predicts and what the alternative hypotheses predict. The two numbers that tell us this are called likelihoods, and they are the probability of the observation if the hypothesis were true, and the probability of that observation if the hypothesis were false.
In the example above, the hypothesis we are testing is that a person has the disease, and the alternative to this hypothesis is that they do not have the disease. The prior was 1 in 1,000, or 0.1%, which was the probability that a given person has the disease before we did any testing. Then we make an observation: a positive test result. The other two numbers we now need are the likelihoods, which are 90%, the probability of getting a positive test result if the hypothesis is true (the person is in fact sick) and 10%, the probability of getting a positive test result if the hypothesis was false and the person is healthy. (This is because for healthy people the test is right 90% of the time, so it must be wrong the other 10% of the time). To correctly determine how probable it is that you have the disease requires all three ingredients: the prior probability and both likelihoods.
When we combine these numbers the right way, using Bayes theorem, we update the prior probability to a new probability called the posterior probability. This posterior is our new degree of belief that the hypothesis is true after observing some relevant information. The posterior probability also becomes the prior probability for the next time we get some new information, and we would then update it to an even newer value. This is how rational beliefs change as we encounter new information.
