Imagine you’re faced with an important health decision about how to treat an illness you’ve come down with – we’ll call it conditionitis. Your doctor offered to write you a prescription for some medication which can often help with conditionitis, but you don’t like to take medication unless you absolutely have to.
Then a friend tells you about a natural treatment for conditionitis that they recently read about on the internet called ionized herb oil. It’s promoted as an all natural alternative to conventional medical treatments.
Not one to believe everything you read on the internet, you decide to do your own research into ionized herb oil. You google it and find plenty of people raving about how well it works and how much they love the product, but also plenty of pages where people are skeptical of the claims. Feeling like google hasn’t been much help, you decide to dig right into the scientific literature.
After a little searching, you find a well conducted study on ionized herb oil from a prestigious university. The study says that they examined 800 people who had recently suffered from conditionitis. 400 of them had taken ionized herb oil, and 400 hadn’t.
For the people who took the ionized herb oil, 200 got better within a week and 200 did not. For the people who didn’t take anything 160 recovered within a week and 240 did not:
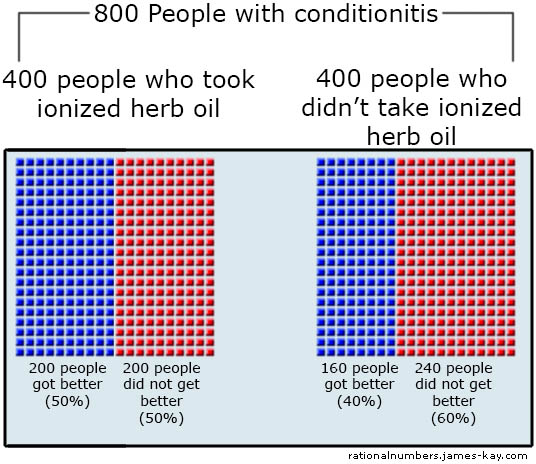
The choice you’re trying to make is whether or not to try this treatment. From this data it appears that if you do there’s a 50% chance that you’ll be better in a week, and if you don’t there’s only a 40% chance. The group given the treatment did better than the control group. So, clearly this stuff does have some beneficial effect…right?
Reading further you find that the study also kept track of the gender of the participants. This could be helpful information as well. Here is the same data from the same study but broken down by gender:
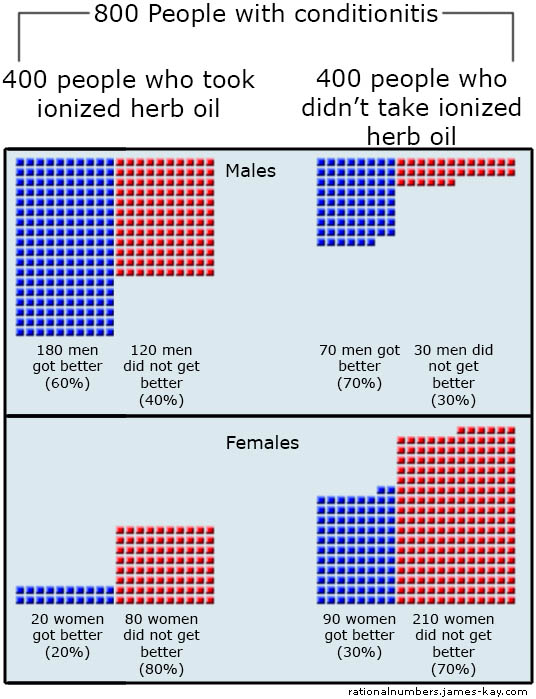
Here we can see that for males who used the treatment 60% got better within a week and for those who didn’t 70% did. For females who used the treatment 20% got better and without it 30% did. And suddenly the treatment doesn’t look effective…for either gender.
So the same data seem to indicate that overall people were better off with the treatment, but that people of either gender were worse off when they used the treatment.
This should seem confusing.
Intuitively, it seems like the laws of mathematics shouldn’t allow this to happen, but they do. Reread the numbers above and add them up yourself as many times as you need to convince yourself that the math is correct. This is a real statistical effect known as Simpson’s Paradox. And if this hasn’t confused you enough yet, consider that if you broke the gender-specific data down further – by age, for example – it could all reverse again, and it might look like the treatment is effective overall, ineffective for either gender, and effective for any age group of either gender.
It’s also not just some clever numerical trick that can’t actually happen in real world examples. The example above may be made-up, but here’s another instance of the same thing occuring in sports. Below are some real statistics from the April 27th 2011 NBA playoff game between the Memphis Grizzlies and the San Antonio Spurs:

Notice that the Spurs made a higher percentage of both their 3-point shots and their 2-point shots, but if you add them together the Grizzlies made a higher percentage of their shots overall. This doesn’t seem mathematically possible, but add up the numbers yourself if you like, or go check the official game stats. Yes, this can really happen.
Now the big question of course is, what is the explanation? Which team shot the ball better? Does the study show that ionized herb oil makes conditionitis better or worse? The answer is…
…well, it’s complicated.
Some will be disappointed to learn that the point of this article is not to explain how this can happen, or to teach the reader how to actually determine cause and effect. The purpose of this article is to shatter the illusion that it’s easy or straightforward to interpret causality from statistical information. Working out cause and effect from simple statistical data can seem easy, straightforward and intuitive, but it’s not.
We’re often reminded that correlation does not imply causation[1], and given examples that make this obvious. Ice cream sales and drownings are correlated, but it’s obvious that these don’t cause each other; rather both simply occur more during the summer. It’s important, however, to watch out for cases where it’s not so obvious that causation is not implied. One might think that the ice cream example is a typical case where you can’t infer causation, but that the results of the observational study on conditionitis are somehow a different kind of statistical data that do prove causation.
People can often get things very wrong when they try to read advanced material from a field before they understand the basics, and this matters today because so many people – often driven by a distrust of science and medicine – insist on “doing their own research”. If your doctor tells you not to take ionized herb oil for your conditionitis, but you look up a study and the numbers say that more people got better when they used it…well, no wonder some people begin to suspect a conspiracy. Learning is something that should never be discouraged, but wading into the deep end of a subject before learning to swim can often lead to mistaken ideas and incorrect understandings rather than learning.
For those who are really interested in understanding when we can say the conditionosis treatment works and when we can’t, try the excellent book Causality by Judea Pearl. This author’s work, the causal calculus, has revolutionized the sciences, and has the power to say when we can and can not determine cause and effect from statistical data. But for the rest of us, confusion is the appropriate response to the examples above. It’s better to know that we don’t understand cause and effect than to feel as though we’ve learned something when we haven’t.
