In 2002 a company called ZeoSync announced that they had created a ground-breaking new piece of data compression software. Data compression software was nothing new – .zip files had been around since 1989 – but ZeoSync claimed their software could outperform competing products by a vast margin.

ZeoSync’s extraordinary claim was that their product could compress arbitrary data. Other data compression schemes, like .zip, could compress some data down to a size much smaller than the original data, but other data wouldn’t end up much smaller at all, or would actually end up larger. ZeoSync, however, claimed that they could compress any data at all^[1].

Soon their claims were met with doubt and skepticism from information technology experts who said that ZeoSync’s claims were impossible. ZeoSync responded by promising to prove their claims soon by releasing demonstration products.

Now, put yourself in the position of an average layperson in 2002. Imagine you were a journalist trying to cover this story, or an investor trying to decide whether to take a risk investing in this company. How could you make a decision about who to believe?

On the one side, ZeoSync had patents on their software, and had several well-known mathematicians working for them. The company even listed as a consultant mathematician Steve Smale, a winner of the Fields Medal which is like the Nobel Prize of mathematics. Their press release was filled with very complicated and technical-sounding explanations of their technology:

“ZeoSync intentionally randomizes naturally occurring patterns to form entropy-like random sequences through its patent pending technology known as Zero Space Tuner™. Once randomized, ZeoSync’s BinaryAccelerator™ encodes these singular-bit-variance strings within complex combinatorial series to result in massively reduced BitPerfect™ equivalents.”

-ZeoSync Press Release^[2]

On the other side were experts with equally compelling qualifications. They said ZeoSync’s press release was just meaningless marketing mumbo-jumbo. They claimed that ZeoTech’s claims weren’t theoretically possible. They said they didn’t need to know any details about the software; they knew it couldn’t work as claimed^[3].

A layperson caught in the middle of this controversy would have great difficulty deciding which side to believe. Without an understanding of the subject, “I don’t know” really is about the best one could rationally say. But now, lets see how we can do better by learning a little bit about information theory and see how that changes the picture.

We’ll begin with a very simplistic introduction to how data compression works. Imagine you have some data storing an image, such as the following simple image consisting of just nine pixels:

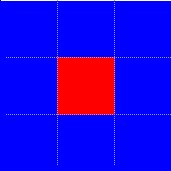
This image could be represented as a sequence of words describing the color of each pixel in some order. Such a description might look like this:

blue, blue, blue, blue, red, blue, blue, blue, blue

It takes nine words to represent the image this way. Now, if we wanted to “compress” this image data we could invent a rule that lets us describe the same image using fewer words. For example, our rule could be that if a color is repeated we can just say how many times it is repeated instead of saying the color over and over again. Now we can represent this image using just five words instead of nine:

four blue, red, four blue

We have compressed our image from nine words down to five words, but notice that this won’t work for all images we could have started with. For example, in the following image there are no repeated colors, and so our rule doesn’t let us represent it with less data; we still need nine words to represent it:

This is a very simplistic description of data compression (data on a computer aren’t stored using words but using bits) so now consider a more realistic example. Imagine we have four bits of data. A bit is either a one or a zero, so our data could be any sequence of four ones and zeroes like “0010″ or “1011″. There are only sixteen different ways to arrange four ones or zeroes, so whatever data we have must be one of the following:

0000	0001	0010	0011
0100	0101	0110	0111
1000	1001	1010	1011
1100	1101	1110	1111

Now, if we want to compress this data, all we need to do is to come up with a rule for taking the data and turn it into a smaller amount of data in a way that doesn’t lose anything important. Then to get our original data back, we just need to apply the opposite rule, which will take the smaller data and give us back our original data.

One possible rule could be “Remove any zeroes from the beginning of the data“, so if our data was “0010″, this rule would remove the two leading zeroes, turning it into just “10″, and thus compressing it down from 4 bits to just 2 bits. To get our original data back we apply the opposite rule, which in this case is “add zeroes back onto the beginning until it’s four bits long again”.^[4].

If for some reason we needed to remember the data “0010“, our rule lets us just remember “10” which is much shorter. Then when we want to know what the original data was, we just apply the decompression rule and get back “0010“. In this case compressing and decompressing the data looks like this:

Now, notice that just like when we compressed the image data before, the rule won’t always make our data smaller. For example, if our data didn’t begin with a zero at all, like “1011“, there are no leading zeroes to remove, and so it is still four bits long even after we apply our rule:

This turns out to be not just a limitation of the compression rules in these examples, but a limitation of any compression rule. Here’s the reason why: say we wanted a rule that could take any four bits of data and compress it down to just three bits. Any four bits of data must be one of those sixteen possibilities we saw above, but for three bits of data there are only eight different possibilities:

000	001	010	011
100	101	110	111

If we compress four bits of data down to three bits then the compressed data must now be one of these eight possibilities…but these eight obviously can’t represent all sixteen of the larger data sets. If you apply some decompression rule to these eight different three-bit data sets you can only get back eight different four-bit data sets. That means there are still eight other four-bit data sets that you can’t get back by applying the decompression rule to any of the three-bit data sets.

This is known as a counting argument, and the argument applies just as well for data of any size. For any rule that can compress some data, there is always other data that the rule can’t compress. The counting argument tells us that there is no data compression scheme that can compress every data set, even by a single bit. This is why ZeoSync’s claim is impossible.

If you take this idea to the extreme, this becomes pretty obvious. If there was any software that could truly compress any data, then you could take some data and compress it, and then compress the compressed data again, and then compress that data again, over and over and keep getting a smaller amount of data each time. You could do this until you’re down to just one bit of data – a single one or zero. But obviously there’s no rule that would let you take just a single one or zero and somehow, working from only that one bit of information, reproduce all of the original data!

So now, with a basic understanding of the relevant information theory, does it still seem like ZeoSync’s product might have done what they claimed? Do you still wonder which side of the “controversy” was right? Does investing money in ZeoSync seem even remotely sane?

Are you even slightly tempted to apply the word “controversial” to ZeoSync’s claims anymore, or does “nonsense” or even “fraud” seem more appropriate now?

When something is controversial, sometimes that means that mankind simply doesn’t have a complete understanding of the subject yet, and that even the experts at the forefront of our knowledge are struggling to understand it. There are some questions at the frontier of physics – for example, about quantum mechanics or string theory – where even our best understanding doesn’t point to a clear answer yet.

Other times – as was the case with ZeoSync – there isn’t a controversy because the knowledge doesn’t exist, but merely because there are some who don’t understand the current state of our knowledge. By 2002 we had possessed all the theory and reasoning needed to tell us that ZeoSync’s claims were impossible for over fifty years. Those who claimed otherwise did so out of an ignorance of our best understanding.

The same is true of many other “controversial” subjects. People that don’t understand the relevant physics often claim to have built perpetual motion machines or devices that produce reactionless thrust using gyroscopes. The fact that people make these claims could lead a layperson to believe that our state of knowledge is uncertain about these subjects, but in fact there are few things science is less certain about than the impossibility of devices like these.

Some people still believe that the earth is flat and even make serious technical arguments for this position against stupendously embarrassingly monumentally overwhelming evidence to the contrary. Does that make the shape of the earth controversial?

By now you can probably guess what became of ZeoSync. Steve Smale soon clarified that he was not closely involved with the project, and did not endorse the company’s claims. They never released the demonstration products they promised, and in a couple of months their web site disappeared, and they were never heard from again.