When a result is given as a percentage, this can sometimes give you small clues about the quality of the underlying data. Have you ever read a claim like
“25% of those polled said that…”
or
“67% of the samples tested positive for…”
and thought to yourself, “Hmm…those percentages are suspiciously close to fractions like one quarter or two thirds?”
A claim that 67% of soil samples taken in a particular area tested positive for contamination might mean that 400 samples were taken and 268 of them tested positive, but it could also mean that just 3 samples were taken and 2 of them tested positive. In both cases this works out to 67%, but the first case actually represents vastly more information than the second one does.
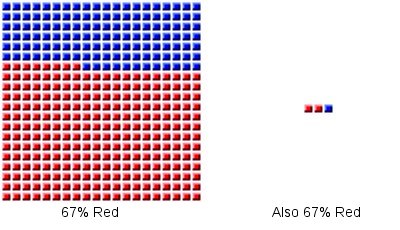
If such a claim appeared in a proper scientific publication you could simply read the article and all the relevant details, including the number of samples, would usually be stated there. Scientists know the importance of having an adequately large sample, and a paper that omitted this information is rather unlikely to be published. In less scientific settings, especially where persuasion is the goal rather than knowledge[1], the sample size is very often not available.
But all is not lost, because not all percentages are created equal. Without any context there’s no way of knowing from a statement like “50% of veterinarians recommend brand A dog food” if they actually polled more than two people to determine this number. A claim like “75% of dentists use toothpaste brand B” could very well be the result of a survey of just four dentists. Numbers like 20%, 40%, 60% and 80% could be describing a group as small as just five items.
On the other hand, if you hear that “26% of people polled preferred candidate A“, you can actually know just from that result alone that they polled at least 19 people. If the percentage was 34% you would know that they polled at least 29 people. A percentage of 51% would imply that they polled a minimum of 35 people.
This is because there’s simply no fraction with a denominator less than 35 that works out to 51% (when rounded correctly). If you have a sample of 35 people and 18 of them are female, that’s 51%, and all other ways to get the number 51% involve a sample of more than 35 things.
If you have 55 marbles and 28 of them are blue that’s 51%, or if you shoot a basketball 119 times and score 61 times that’s also 51%, but there’s simply no way to get the number 51% with fewer than 35 things. For example, imagine you have 34 pieces of fruit. If 17 of them were apples then your fruit is 50% apples. But if 18 of them were apples then your fruit would be 53% apples. There’s no whole number of apples which could represent 51% of the group, and the same is true for any other number smaller than 35.
For any given percentage there’s a minimum sample size implied by that percentage. By calculating all of these we can construct a table of them.

When a percentage has a lower number we could say this makes that percentage more “suspicious”, especially if the claim is already coming from a dubious source, because it’s possible that it’s based on an unreasonably small sample. (In the table above, colours closer to red imply more “suspicious” percentages. The colour scale is logarithmic.)
The table above only works if a percentage is rounded off at the decimal place. If a percentage is rounded off after one decimal place, like “89.7%“, this can actually give you a lot more information about the sample size, and in many cases places the minimum sample size well over a hundred. For example, the number “28.5%” implies a sample size of at least 123, and “57.2%” implies a sample size of at least 138.
A table of the minimum sample sizes implied by percentages rounded after one decimal place can be found here[2].
Remember, a percentage with a low minimum sample size doesn’t necessarily mean there was a small sample size, it just means if could be from a small sample, but percentages with a higher number definitely weren’t taken from a very small sample.
